Readers of this blog, of which I am certain there are few, will know that I am not an easy mark and that nothing delights me more than taking the sails out of the windbags who pronounce themselves “experts.” At the same time, I do respect those who have dedicated themselves to using actual evidence to advocate for certain policies. So it saddens me to poke huge holes in Jo Boaler’s defense of the Common Core as described in her opinion piece for the Hechinger Report.
This is definitely not Boaler’s best work, and after digesting it, I have reached the conclusion that it was either penned by someone who wants to discredit Boaler’s work, or that Jo herself just wasn’t up to her best form that day (which I imagine happens occasionally….)
Let me just say this: Jo Boaler makes several statements that are majorly incorrect. I’m sorry, but it’s true: they’re wrong. Not that there’s anything wrong with that. And it’s not like I’m trying to start an argument, because, well, it’s not like I’m brilliant or anything. In fact, whenever anybody admits that I am correct, I write it off to the fact that even a broken clock tells the correct time twice a day.
So it’s not that I am right; rather, it is just that many of the statements that Jo Boaler makes are wrong.
The piece, “Memorizers are the lowest achievers and other Common Core math surprises”, which was published last May (I’m sorry, but I’m a little slow to catch up on these things,) appears to make some interesting points, but truth be told, many of Boaler’s assertions lack validity and some of her statements are just illogical. While some of my points may appear to be nitpicky, others are a lot more serious, which makes this all the more difficult to write.
Let’s begin with the opening paragraph: I have encountered a lot of propaganda advocating for the Common Core, but none of it has ever referenced connections between its development and brain or learning sciences; in fact, not a single member of the Common Core working group has any experience with learning or brain sciences. If the authors of the Common Core did incorporate these findings, it must have been imaginary, because as someone who has spent a lot of time investigating educational research and incorporating it into my teaching practice, it appears to me that the CCSS was written without any regard for contemporary findings in educational, psychological, cognitive or neurological research.
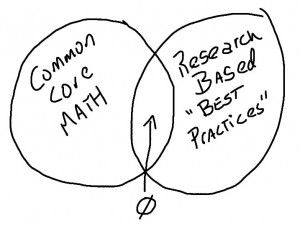
CCSS and Educational Research: Dubious Connections?
In fact, for many experts, the CCSS are actually contradictory to what neuroscience and learning sciences have to say is “good practice.” According to a joint statement by members of the National Association for the Education of Young Children, the K – 3 standards, which form the bedrock of mathematics education, are wildly out of touch with our understanding of how the young brain learns and understands mathematics. The NAEC statement opposing the CCSS for K – 3 learners was signed by none other than the three past presidents of that organization, as well as noted scholars like Howard Gardner of Harvard University. Jo Boaler, I respect you, but that’s massive opposition to the foundational years of mathematics as envisioned by the authors of the Common Core.
I agree with Boaler (and who wouldn’t, in this day and age?) that children learn math in many different ways, but to say that “mathematics classes of the past decade have valued one type of math learner, one who can memorize well and calculate fast,” is just plain incorrect. I’ve been working in mathematics education for over 30 years, and I can assure Dr. Boaler that this has been an issue since I began my career way back when. In fact, I remember that memorizating and calculation were part of my “mathematics” education growing up in the 60’s, which takes us back a half-century. Stating that this is a problem that just popped up during the last 10 years is more than dismissive, it is pure fantasy.
Moving along to the next paragraph, Boaler cites statistics from the PISA exams as evidence that the lowest achieving students approach math through memorization of steps. First of all, PISA is a terrible source of data from which to draw any kind of interenational comparisons, as it does not take into account references to issues like poverty and educational culture. Should we really be comparing the scores of students in Singapore, a high-performing city-state that has fewer school aged children than the NYC school system, a poverty rate that is 1/3 of the United States and boasts a culture where 97% of all students attend out-of-school programs to boost their academic achievement? I have issues with using the PISA study to reach any conclusions, including the current infatuation with something called “Singapore Math.”
Furthermore, it is not clear which part of the PISA results Boaler used to fabricate her assertion that students who rely on memorization are also the lowest achievers. Her link references the entire PISA report, which includes dozens of pages of Excel worksheets; it is not at all clear which sets of numbers support her conclusion, and whether they are statistically valid or reliable. I would like her to elaborate on which data points she used to reach this very important conclusion (which I hope is true, by the way…..)
Additionally, while there may be a correlation between “memorizers” and low achievement, Dr. Boaler, who I’m sure is quite conversant in statistics, would be the first to admit that this doesn’t necessarily indicate causation. That is, it could be the case that low achieving students struggle with poor memory, rather than memory driven instruction leads to underachieving students.
Finally, as someone who, like me, is suspicious of standardized testing in all its forms, I’m surprised that Boaler herself would rely on PISA scores to support this position. Surely there must be some better data available that proves this case; if not, perhaps we can put some of those Stanford grad students to work on it?
Some of Boaler’s statements are just mathematically illogical. “The past decade has produced a generation of students who are procedurally competent but cannot think their way out of a box” makes no sense – how could ten years of education produce 20 years of students (a.k.a. “a generation”) who are “non thinkers?” With this statement, Boaler is implying that in 2005 some kind of cataclysmic change happened in mathematics education that is only being rectified by the Common Core, which was released in 2010. I was teaching in 2005, and I don’t recall an educational earthquake of the kind Boaler describes. Perhaps I missed it?
Additionally, since the CCSS math standards were released in 2010, and if we assume it took 2 more years to get them into schools (2012), then the last three years of underachievement (2012 – 2015) which Boaler cites can be blamed on the use of the Standards themselves. Now I know that this is completely wrong, but I think it shows that Boaler’s repeated claim about this issue taking place during the “last decade” is illogical.
Oddly enough, for a piece that trots out the importance of advancement in brain sciences, there is not a lot of factual information about what neuroscience says about learning mathematics. For example, Boaler states that memorizing multiplication facts does not prove that one is “advanced” mathematically, but never states why this is true. Stanislaw Dehaene, in his wonderful book “The Number Sense,” does provide us with an explanation: multiplication facts are stored in the basal ganglia of the brain, which means they are remembered “linguistically.” He goes on to state that this is also the part of the brain which memorizes things like song lyrics, nursery rhymes and prayers. Thus, Boaler is correct when she states that recalling multiplication facts is not in and of itself a mathematical process, but used no evidence to back this up.
At the same time, Boaler seems to imply that there is no need for children to memorize multiplication facts. I have to disagree, and I think most classroom teachers who teach constructivist mathematics would take a similar position: there is nothing more frustrating than watching a 5th grader attempt to analyze the pattern 1, 3, 6, 10, 15 and demanding a calculator to find the difference between the different numbers. Just as we acquire “sight words” so that we don’t have to sound out “or” and “and” every time it comes up in a sentence, we need a certain amount of “sight computation” to reduce the cognitive load to do other kinds of mathematical activities.
I’d like to go on, but I think the evidence I’ve presented above more than makes my case. I invite Dr. Boaler to dispute and/or clarify what she wrote in her piece, because I am, after all, one of her earliest supporters and biggest fans (she even autographed a copy of her book “What’s Math Got To Do With It” for me at an NCTM conference, which I treasure.) I hope she’ll read this with an eye towards better supporting a set of policies with which I, for the most part, agree.
A disclaimer: I am not aligned with nor am I sympathetic to the views of R. James Milgram and Wayne Bishop, who I believe are the troglodytes of the math education world. I am concerned that Boaler, who I know and admire as a tireless advocate for what “good” math education looks like, is discrediting herself by shilling for the Common Core, and supporting it with information that is both inaccurate or poorly sourced. I hope she’ll retract this misleading piece of writing and replace it with something that is more representative of her mostly excellent work.
