In my previous rant, I went on and on about the cruddiness of math workbooks and how teachers come to rely on them for exercises for their students. However, the truth behind these workbooks is that they are rarely written by actual mathematics educators. In fact, they are usually assigned to the bottom feeders of the publishing industry, and there is little to no actual professional oversight of the content.
I’ll cite one example, which is drawn from the Go Math! third grade workbook, which a group of about a dozen kids were laboring through while their teacher led a “mini-lesson” at the other end of the room:
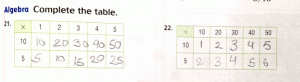
A Trig Table: Readable in any direction!
These poor kids: they thought the second table was also about multiplication, but the “authors” switched the operation to division. Here’s the problem: it is not clear which order you are supposed to do the division, because the point of a “table” is that it is supposed to be independent of “order” – addition, multiplication, distance (or any other table for that matter) should be able to be read without need for knowing the “direction.”
But since we have the table, and since we read problems with the “÷” from left to right, it appears that we’re supposed to read the numbers in the column first and then the row. But that doesn’t make sense, as these kids are third graders, and they don’t know what 10 ÷ 50 would mean……
But division, as we all know, is not commutative, a property which 3rd graders are just figuring out. We have to assume that the upper row is the dividend and the numbers in the left column are the divisors because the dividend is supposed to be bigger than the divisor (at least, in order to make sense if you are in third grade), but if we do assume this, that violates a fundamental principle of concept development: you can’t state a principle unless it is universally true. Dividends are bigger than divisors in only a limited number of contexts; in fact, the size of the two numbers has nothing to do with determining which is the divisor or dividend – that is dependent on something called “context.”
Yes, in 3rd grade, children do usually encounter dividends are larger than divisors, but they can also be equal (20 ÷ 20 = 1) and they can be smaller (0 ÷ 1 = 0) (and all these examples were on the same page of the workbook, btw.)
The point of this rant is that this is an example of cruddy workbook content; the authors called it “algebra” under the misguided notion that this is what an algebraic table might look like a few years down the road (it won’t), but instead it is confusing and the poor children who were left to attempt this on their own were completely baffled by the task. The only thing that cleared up this confusion was that I happened to be visiting the classroom that day. Really, is this content “safe” enough to be left alone with children?
