As followers of my blog know, I’ve been working on better ways to teach math for almost 30 years, and just when I think I’ve seen everything, someone has to come along and show me a different approach. It’s rather humbling, but I guess I can take some credit, because as Picasso once opined “good artists borrow; great artists steal…”
For some (many) years I’ve worked with children on creating number patterns using the hundreds chart, usually in the form of skip counting, which reveal all kinds of interesting vertical and diagonal lines, plus the “knights move” (2 down and over 1, or some combination thereof), which leads into all kinds of fascinating discussions on classifying and grouping skip counting patterns. The results don’t look a lot different year after year:
This morning I happened to stop by the classroom of our 3rd grade teacher who goes by the name Nancy S., and as we were exchanging our Rosh Hashanah greetings, she showed me an activity where she took this concept and turned it on its head: instead of starting with a “rule” (like skip counting by 3s shown above), why not have the children create a visual pattern of their own, and then describe one another’s “rule.”
Here are some of the examples:

Below each of the patterns is a small piece of paper with a few sentences in which a student who didn’t create the visual pattern writes his/her hypothesis of what the originator was thinking when he/she created this number pattern.
Suffice to say, this activity fits into so many of the ways I like to think about what an exemplary math activity is about: it takes a small idea (that number patterns can be visualized on a hundreds chart) and turns it on its head. Implicit in this activity is the idea that mathematics is about communicating through different modes: we start out with a visual representation that may be purely visual (that is, the student decides to fill in an entire column or diagonal row of numbers), or may follow a rule (“fill in all the numbers where the ones and tens adds up to 9”) and then leaves it to another person to decipher what he/she was doing. It’s a neat application of the “what’s my rule” activity where students look at a series of relationships between numbers (“3 in, 4 out; 4 in, 5 out, 6 in, 7 out; what’s my rule?”) but this time they are looking at visual relationships and then by decoding the numbers, they can turn it into a verbal relationships.
What also resonates for me is the current research that looks into mathematics achievement and relational thinking; that is, there is considerable evidence that facility with numbers comes from the ability to develop narrative facility, particularly when it comes to switching perspective between different characters in a story. If we extrapolate this idea, then developing mathematical thinking comes from continually switching perspective between not only characters in a story, but problems that have been posed to you. That is, we refine our mathematical thinking both by posing problems to others, and by attempting to interpret the problems that have been posed to us. This is best facilitated by removing the teacher from the equation, and working “peer to peer,” because when children are attempting to communicate ideas to other children, they will take on the perspective of another child, rather than communicating “this is what the teacher wants.”
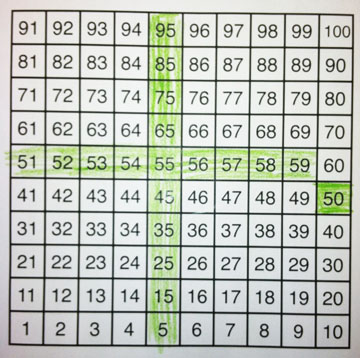
Where to go from here? Well, I couldn’t help but get into the act, being the devil I am: I printed up my own hundreds chart (which you’ll notice counts “up” instead of “down”) and filled in a pattern and sent it over to Nancy’s class. What’s going on in my mind?