As many of you may (or may not) know, I have an exhibit on Governors Island in New York Harbor that will be on view until the end of September. For those of you not familiar with Governors Island, it was originally the home of the governor of NY when it was still a colony; in its 200+ year history it has been an army base, jail for Confederate soldiers and, from 1966 – 96, a Coast Guard base that housed approximately 3,500 soldiers and their families. Now under the ownership of the City of New York, it has become a multi-purpose space for arts and recreation.
In January, I applied to the Trust for Governors Island to obtain a space to install my exhibit, Mü-Math: The Mobile Unit to Promote Mathematical Thinking on Governors Island from Memorial Day to September 30th, when Governors Island will be closed to the public until the following spring. The exhibit is housed in a building that used to be apartment housing for soldiers with families: by New York City standards it is quite spacious, with two bedrooms, a large kitchen and living room.
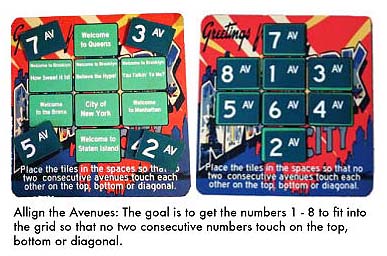
The exhibit has about 10 different activities which are notable in that they are more like puzzles than the math you would find in a textbook, yet each is linked to powerful ideas about the nature of mathematical thinking. For example,the idea of algebra as pattern detection, interpolation and extrapolation is conveyed using a set of subway cars that show a number progression. Each week I try to add a new activity to spice things up; the latest idea, “Align the Avenues,” actually came from a visitor who presented me with a puzzle where the numbers 1 – 8 had to be put into a grid so that no two consecutive numbers would touch on the top, bottom, sides, or diagonals. I re-cast the numbers as “avenues” and turned the grid into the “Welcome to ______” road signs that greet drivers on our various highways and bridges, so that it now looks like this:
Unfortunately, as I write this, I realize that the directions don’t specify the sides as well, but that can easily be corrected in the final version. Yes, I know the “solution” on the right is incorrect, but if you do decide to solve this on your own, please look at the solution carefully. There is real elegance to where certain numbers are placed, and it begins by thinking about which numbers have the fewest “neighbors” and how that should influence their placement. The solution also has an interesting train of logic that one must follow, because one “clue” leads to another, which leads to another, which finally solves the puzzle. As in any great puzzle, there are multiple solutions, but they all follow the same kind of internal logic.
Of course, if you’re hosting an exhibit on mathematics and problem solving which incorporates puzzles, you’re going to attract a certain number of “wise guys.” Here’s one that a character sprang on me (and a roomful of visitors) a few weeks back. He claimed to have invented it and uses it as a “test” to figure out whether one has the skills to be a leader. I flunked it with flying colors, so maybe my future is limited to being a self-described cognitive artist.