It was back during the latter days of the Clinton Administration when I was hired for my first position as an elementary level math coordinator. This came after teaching middle school mathematics for the previous 15 years as well as earning an M.S. in elementary mathematics education. The fact that I had not spent a lot of time working with kindergarten through 4th grade children did not seem to deter the hiring committee, perhaps because there were not a lot of people who had expertise working with young children in mathematics. After all, if you were interested in mathematics, why would you want to work with little kids?

Is this all we can expect from elementary school math?
After a few weeks visiting classrooms and observing children at work, I was quickly disabused of the notion that there was not a lot happening in these classrooms. The concepts the students were working on were very complex and, as I spent a considerable portion of my day working with them one on one, there was a lot more that could be done with them beyond counting and making simple patterns. As I worked alongside teachers, I pointed out ways that their mathematics lessons could be richer, more engaging and challenging, while still reaching its intended audience. What I realized is that my previous 15 years of middle and upper school mathematics teaching was not a liability, but an actual advantage: Not only did I know what mathematics students would encounter a year later, but I had the additional foresight to know what these same children would learn 5 – 10 years down the road.
During this period of revelation, I found myself on a car ride with a colleague who taught in the the school’s high school program. As we were driving along, this teacher candidly stated her opinion of my professional work: “I don’t know why we need a lower school math coordinator; after all, aren’t these kids only learning how to add and subtract?”
I held my breath for a few minutes, and then, releasing it slowly, I suppressed my best Dan Akroyd imitation. I calmly explained to her that the children at our school would learn more about mathematics between the ages of 5 and 10 than the entirety of their lives thereafter. It reminded me of Hillel’s dictum about studying Torah: whatever is abhorrent to yourself, do not do unto others. Everything else is commentary….

Everything this man knows about mathematics he learned in kindergarten….
If you think about it, all of advanced math is essentially an elaboration of what a child will learn in elementary school. Algebra is a generalization of arithmetic, while trigonometry builds upon the concepts of ratio and proportion. If you’ve read Dr. Seuss’s “The Cat in the Hat Comes Back,” where Cats A through Z are half the size of each succeeding iteration, then you will understand that he is describing the concept of a limit, from which we get, yes, calculus. Children’s literature is filled with descriptions of advanced mathematics, whether it is the concept of exponential growth described in “One Grain of Rice,” to the “crypto-arithmetic” problems posed in “More Sideways Arithmetic From The Wayside School.”
At the same time, there was plenty that had to be accomplished during the elementary school years when it came to the essentials of reading and writing numbers, as well as solving simple addition and subtraction problems. This does not mean that I had to hold back on doing in-depth investigations that would demonstrate powerful analytic tools while developing important ideas.
All of which lead me to develop an exploration that I conduct with the kindergarten class at my school, which involves an in-depth look at the children’s game, “Crocodile Dentist.”

Can this children’s game be a lesson on data, statistics and patterns?
If you are the owner of this game, you know it mixes both surprise and terror: players take turns pushing down one of the lower teeth on this plastic reptile, until the croc “bites” the player who has selected the “dangerous” tooth. The biting tooth changes location each time the game is played, so the surprise comes because the players never know which tooth will bring down the jaw, or whether it will be the first, second or even the last one selected.
The idea of randomization is a fertile ground for exploring mathematics with young children, who are always concerned with the notion of “fairness.” Do all the teeth have the same opportunity to “bite” or do some come up more often than others? Is there a way to predict which tooth will be more dangerous than another, or is the game entirely arbitrary?
I introduced the game by explaining that as someone who is interested in math, this game made me wonder whether a “strategy” could be developed to figure out if some teeth were “safer” to press than others. How would we find out if this was true? This led the class into the concept of “sampling.” It was not enough to play a few games to determine if certain teeth bit more often than others; we would need to play a lot of games, and keep track of which teeth did the biting.
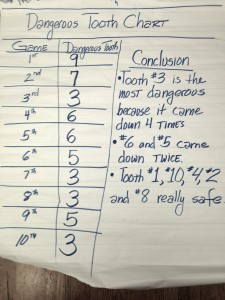
Results of 10 games played by a group of four kindergarteners.
For the next four math sessions, I took a small group of kindergarteners out to play 10 rounds of Crocodile Dentist and recorded the results as a table on a sheet of chart paper:
As we were recording our results, the students learned about some important techniques used in mathematics: we organized the data we collected into a table, and that table is read both vertically and horizontally. They learned about the different kinds of numbers that could be used to describe the game. For example, ordinal numbers show the “order” of things, like the first through 10th game played, while cardinal numbers record the number of times a specific tooth bit us (for example, tooth #3 bit us 4 times.) The also learned that a number could be used to locate a position, which is called a “nominal number.” In this case, there were 10 teeth on the game, and each one specified a certain location in the crocodile’s mouth.

The entire kindergarten class helped crunch the data from 40 “crocodile dentist” games.
The students also learned how to look for patterns in the data they collected: they saw that the same tooth might bite two, three times or even four times in a row, while others may pop up less often or not at all. At the end of each session, each member of the investigating group had to come up with a statement to describe some aspect of the data table we had constructed.
After working with all four groups, we assembled our findings at a “summit” where the 4 posters were displayed, and the class analyzed the results from 40 different games. Looking at the data, the class uncovered specific patterns that could be used to optimize one’s certainty of escaping a bite. For example, tooth #3 came up consistently in all 4 sessions, to the point where in one set of games, it bit us 4 times out of 10 games played. Tooth #2 was even worse: not only did it show up in all 4 samples, but with one group it bit 4 times in a row, for a total of 6 games altogether. This finding developed the idea of a ratios and how they could be compared: tooth #2 was more dangerous than tooth #3, because it came up 6 times out of 10 compared to 4 times out of 10.
The students also found that certain teeth were “safer” than other teeth. For example, tooth #1 was the losing tooth in only 2 out of the 4 sessions, and in those groups, it only bit once each time. Tooth #8 was an even safer bet: it showed up in one of the 4 investigations, and it only bit us once in all 40 games played.
Finally, we saw that while the data could help us make good choices while playing this game, nothing was certain: after discussing our findings, we played a round of Crocodile Dentist using our findings. We avoided teeth like #2 and #3, choosing teeth #10 and #9, which didn’t come up as often in the past. Wouldn’t you know it, but the tooth that bit us during that game was #8, a tooth which had been considered “extremely safe.”
This investigation models what many would consider “good mathematics,” in that it develops powerful ideas in a context that is provocative and relatable. It motivates children to think analytically about something they might otherwise ignore, and, most of all, it’s just a lot of fun. For a kindergartner, “fun’ is the most important attribute to learning about mathematics (and shouldn’t it be for us all?)

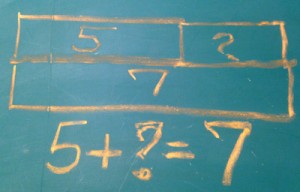
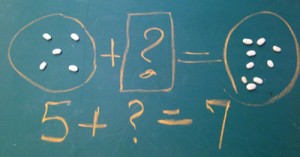 Both models to the right can be used to solve the problem described above. The top one uses a “bar model” which is attributed to the Singapore Math program, but was actually developed by W.W. Sawyer over a half-century ago. By comparing the part (the 5 apples I had on Monday) with the whole (the 7 apples I now have on Tuesday), I understand that I am “adding” on to 5 until I get to 7.
Both models to the right can be used to solve the problem described above. The top one uses a “bar model” which is attributed to the Singapore Math program, but was actually developed by W.W. Sawyer over a half-century ago. By comparing the part (the 5 apples I had on Monday) with the whole (the 7 apples I now have on Tuesday), I understand that I am “adding” on to 5 until I get to 7.


 I have an online “colleague” who makes no bones about the fact that she hates math. She’s expressed this opinion in numerous message threads on a community board to which we both post. She works in science education, and is about the most civil and respected voice as one is likely to encounter on these kinds of open forums. If there is one vice this person possesses (and I’m quite sure it is only this), it is that she continually professes, quite seriously and earnestly, that she hates math.
I have an online “colleague” who makes no bones about the fact that she hates math. She’s expressed this opinion in numerous message threads on a community board to which we both post. She works in science education, and is about the most civil and respected voice as one is likely to encounter on these kinds of open forums. If there is one vice this person possesses (and I’m quite sure it is only this), it is that she continually professes, quite seriously and earnestly, that she hates math.
















